[next] [prev] [prev-tail] [tail] [up]

Capitolo 9
La ricorsività

Livello: Medio

La programmazione in LOGO spesso usa una tecnica chiamata ricorsività. In questo capitolo esploreremo la ricorsività con semplici esempi e disegneremo alla fine una curva frattale chiamata “fiocco di neve di Van Koch”.
Prima di tutto:

Una procedura è ricorsiva se invoca se stessa

9.1 Nell’area di disegno

9.1.1 Un primo semplice esempio


Codice 9.1: Una semplice procedura ricorsiva
Per ex1 
  DX 1 
  ex1 
Fine

Questa procedura è ricorsiva perché la procedura ex1 è invocata nell’ultima riga della medesima procedura. Durante l’esecuzione osserviamo che la tartaruga ruota su stessa verso destra all’infinito. Per interrompere il programma dobbiamo cliccare il bottone di STOP.

9.1.2 Un secondo esempio

Per il secondo esempio impariamo tre nuove primitive:


Codice 9.2: La lancetta dei secondi di un orologio
Per ex2 
  Av 200 CancellaPenna Aspetta 60 
  In 200 PennaDisegno DX 6 
  ex2 
Fine

Il programma ripete la stessa procedura ogni secondo ottenendo i secondi di un orologio.

9.2 Nell’area dello storico dei comandi

9.2.1 Un primo semplice esempio

La primitiva Stampa visualizza del testo nell’area dello storico dei comandi. Stampa si aspetta un argomento, un elenco o una parola.
Per esempio: Stampa "hello Stampa [Essere o non essere] (non dimenticare le virgolette "quando vuoi scrivere solo una parola).


Codice 9.3: Stampare un elenco infinito di numeri
Per ex3 :n 
  Stampa :n 
  ex3 :n+1 
Fine

Invoca la procedura ex3 0 e ferma il programma con il bottone di STOP.
Come esercizio modifica il programma per visualizzare i numeri con un intervallo di 2.

Vogliamo ora visualizzare tutti i numeri interi maggiori di 100 che sono divisibili per 5. Dobbiamo solo modificare il programma così:


Codice 9.4: Stampare un elenco di numeri divisibili per 5
Per ex3 :n 
  Stampa :n 
  ex3 :n+5 
end

e quindi invocare: ex3 100

9.2.2 Uscita dalla ricorsione

Tutti gli esempi precedenti vengono eseguiti all’infinito consumando piano piano tutta la memoria disponibile fino a quando XLOGO fermerà il programma. Normalmente, però, la ricorsione viene fermata dal programma stesso quando si verifica una determinata condizione. Esempi di condizioni sono i seguenti esempi:
Se 2+1=3 [Stampa [è vero]]
Se 2+1=4 [Stampa [è vero]][print [è falso]]
Se 2+5=7 [Stampa "vero][Stampa "falso]

Se non ti è chiara la sintassi delle condizioni vai alla pagina della primitiva Se. Il seguente esempio modifica il terzo esempio per interrompe la ricorsione al 100-esimo numero.


Codice 9.5: Stampare un elenco di numeri inferiori a 0
Per ex3 :n 
  Se :n=100 [Ferma] 
  Stampa :n 
  ex3 :n+1 
Fine

Invoca il programma con ex3 0.
Come esercizio puoi modificare il programma per visualizzare numeri interi tra 55 e 350 che sono divisibili per 11.

9.3 L’esempio di un frattale, il fiocco di neve di Van Koch

Utilizzando la ricorsione è molto semplice generare in LOGO alcune semplici curve chiamate frattali in matematica.
Questi sono i primi passi per creare la linea spezzata di Van Koch:

PIC

Come primo passo si disegna un segmento di una data lunghezza.
Come secondo passo:

  1. il segmento viene diviso in tre parti uguali.
  2. un triangolo equilatero viene disegnato sul segmento centrale.
  3. infine il segmento centrale viene cancellato.

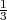A questo punto il segmento originario risulterà spezzato in quattro segmenti di lunghezza pari ad 1 3 di quello originario (terza figura). Il secondo passo viene quindi ripetuto su ciascuno dei quattro segmenti originando 16 segmenti di lunghezza pari ad 1 3 dei precedenti, ossia 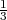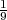1 3 ⋅1 3 = 1 9 (quarta figura). Ad ogni passo la lunghezza dei segmenti si riduce di un fattore 3.
Importante Abbiamo scovato la natura ricorsiva dei frattali!
Vediamo come impostare concettualmente il programma LOGO. Chiamiamo Ln,ℓ il segmento di lunghezza ℓ, corrispondente al passo n.
Per disegnare il segmento:

  1. Disegniamo Ln-1,ℓ∕3
  2. Ruotiamo a sinistra di 60∘
  3. Disegniamo Ln-1,ℓ∕3
  4. Ruotiamo a destra di 120∘
  5. Disegniamo Ln-1,ℓ∕3
  6. Ruotiamo a sinistra di 60∘
  7. Disegniamo Ln-1,ℓ∕3

In LOGO, il programma è molto semplice:


Codice 9.6: Procedura ricorsiva per il disegno di un segmento frattale
  # :l contiene la lunghezza del segmento 
  # :n contiene il numero del passo 
to linea :l :n 
  Se :n=0 [Av :l] [ 
  linea :l/3 :n-1 SX 60 linea :l/3 :n-1 DX 120 linea :l/3 :n-1 SX 60 linea :l/3 :n-1 
  ] 
end

Il programma si invoca come linea 50 3, dove il primo argomento è la lunghezza del segmento originario ed il secondo argomento è il numero di ricorsioni da eseguire. Incredibile il potere della ricorsione!
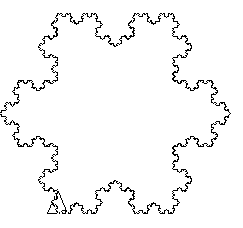
Se disegniamo un triangolo equilatero con tre linee di Van Koch otteniamo uno stupendo fiocco di neve di Van Koch.


Codice 9.7: Fiocco di neve di Van Koch
  # :l lunghezza del lato 
Per fioccoNeve :l :p 
  Ripeti 3[linea :l :p DX 120] 
Fine

Il programma si invoca per esempio con: fioccoNeve 200 6

PIC

9.4 Ricorsione con le parole

Leggi pagina § per capire come impiegare le primitive Parola, Ultimo, e EccettoUltimo, EU.

9.4.1 Leggere al contrario le parole


Codice 9.8: Ricorsione per invertire l’ordine delle lettere in un parola
Per invertiParola :m 
  Se vuoto? :m [output "] 
  output parola ultimo :m invertiParola eccettoultimo :m 
Fine

Si invoca con Stampa invertiParola "Logo.

9.4.2 I palindromi

Un palindromo è una parola o una frase che si può leggere in entrambi i sensi (esempi: I treni inerti, Etna gigante …). Aggiungiamo una semplice verifica all’esempio precedente per capire se la parola o la frase è palindroma.


Codice 9.9: Verificare se una parola è palindroma
# Verifica se la parola :m e’ palindroma 
Per palindromo :m 
  Se :m=invertiParola :m [output vero] [output falso] 
Fine

9.4.3 I numeri palindromi

Anche i numeri possono essere palindromi, per esempio 4884. Infine, un programma per cercare numeri palindromi a partire da un qualsiasi numero (Grazie Olivier SC):


Codice 9.10: Scovare numeri palondromi
Per numeroPalindromo :n 
  Se palindromo :n [Stampa :n Ferma] 
  Stampa (elenco :n "Piu’ invertiParola :n "uguale somma :n invertiParola :n) 
  numeroPalindromo :n + invertiParola :n 
end

Si invoca con numeroPalindromo 78:

78 Più 87 uguale 165  
165 Più 561 uguale 726  
726 Più 627 uguale 1353  
1353 Più 3531 uguale 4884  
4884

9.5 Calcolo di un numero fattoriale

Il fattoriale di un numero n è il prodotto dei primi n numeri interi positivi. Per esempio il fattoriale di 5 è definito come:

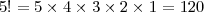
5! = 5 × 4× 3 × 2× 1 = 120
In termini matematici se n è un intero positivo: n! = n × (n - 1)!. Questa relazione spiega la natura ricorsiva del programma fattoriale:
Codice 9.11: La ricorsività nel calcolo del fattoriale
Per fattoriale :n 
  Se :n=0[output 1][output :n*fattoriale :n-1] 
Fine

Si invoca con Stampa fattoriale 5.

9.6 Calcolo del pi greco per approssimazione

Possiamo approssimare il numero pi greco utilizzando la formula:

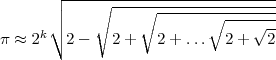
┌ ---∘----------------------- ││ ∘ ------∘-------- π ≈ 2k∘ 2- 2 + 2 + ... 2 + √2--
dove k è il numero di radici quadrate. Maggiore è k, migliore risulterà l’approssimazione di pi greco.

La formula contiene l’espressione ricorsiva 2 + ∘ ------∘-----√--- 2+ ... 2 + 2, quindi ecco il programma:


Codice 9.12: Approssimazione del valore del pi greco
# k e’ il numero di radici quadrate 
Per approxpi :k 
  Stampa [Approssimazione di pi greco:] 
  Stampa (potenza 2 :k) * RadQ (2- RadQ (calc :k-2)) 
  Stampa "------------------------- 
  Stampa [Esatto pi greco:]  Stampa pi 
Fine 
 
Per calc :p 
  Se :p=0 [output 2][output 2+RadQ calc :p-1] 
Fine

Si invoca con approxpi 10.

Con 10 approssimazioni troviamo i primi 5 decimali! Se vuoi trovare più decimali devi aumentare la precisione aumentando il numero di decimali con la primitiva ImpostaDecimali.


Codice 9.13: Il pi greco con 100 decimali
ImpostaDecimali 100 
approxpi 100

E ora abbiamo 39 decimali esatti…

[next] [prev] [prev-tail] [front] [up]