Capitolo 13
Argomento: approssimazione probabilistica di pi greco

Livello: Avanzato

Nota: Alcune nozioni matematiche elementari sono necessarie per questo capitolo.

13.1 MCD (Massimo Comune Divisore)

Il MCD di due numeri interi è l’intero più grande che divide entrambi i numeri senza resto. Per esempio il MCD di 42 e 28 è 14, il MCD di 25 e 55 è 5, il MCD di 42 e 23 è 1.

Gli interi a e b si dicono coprimi o primi tra loro se non hanno un fattore comune eccetto 1 o, in modo equivalente, se il loro MCD è 1. Negli esempi precedenti 42 e 23 sono coprimi.

13.2 L’algoritmo di Euclide

L’algoritmo di Euclide calcola il MCD di due interi in modo efficiente (non dimostriamo qui che questo algoritmo è valido).

13.2.1 Descrizione dell’algoritmo

Dati due interi positivi a e b, controlliamo prima di tutto se b sia uguale a 0. Se è questo il caso allora il MCD è a. In caso contrario calcoliamo r come resto della divisione di a per b. Quindi sostituiamo a con b e b con r e ricominciamo l’algoritmo.
Per esempio calcoliamo il MCD di 2160 e 888 con l’algoritmo di Euclide:

Quindi il MCD di 2160 e 888 è 24. Non c’è intero più grande che divide entrambi i numeri (infatti 2160 = 24 × 90 e 888 = 24 × 37)
Il MCD è resto più grande non uguale a 0.

13.3 Calcolare il MCD in LOGO

Una semplice procedure ricorsiva calcolerà il MCD di due interi :a e :b:

Invochiamo la procedure come Print MCD 2160 888 e otterremo il risultato 24.
Nota: è importante porre tra parentesi tonde modulo :a :b altrimenti l’interprete tenterà di verificare la condizione :b = 0. Se non vuoi usare le parentesi scrivi Se 0=resto :a :b.

13.4 Calcolare l’approssimazione di pi greco

Nei fatti un famoso risultato nella teoria dei numeri dice che la probabilità di due interi scelti a caso di essere coprimi è ≈ 0,6079. Per verificare questo risultato possiamo:

• Scegliere a caso due interi tra 0 e 1000000.
• Calcolare il loro MCD.
• Se il MCD è 1, incrementiamo una variabile contatore.
• Ripetiamo questa procedura per 1000 volte.
• La frequenza può essere calcolata dividendo la variabile contatore per 1000 (il numero di prove).

Come prima nota le parentesi attorno MCD Casuale 1000000 Casuale 1000000. Se non ci fossero l’interprete cercherebbe di verificare la condizione 1 000 000 = 1. La stessa espressione si può anche scrivere come: Se 1=MCD Casuale 1000000 Casuale 1000000.

Invochiamo la procedura con test e con un po’ di pazienza otterremo frequenze che si avvicinano al valore teorico di 0,6097:

La frequenza teorica è una approssimazione di .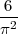

Quindi, se denotiamo con f la frequenza abbiamo: f ≈ da cui π² ≈ e π ≈.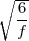

Aggiungo al mio programma una riga che fornisca questa approssimazione di pi greco nella procedura test:

Invochiamo la procedura con test e con un po’ di pazienza otterremo valori di pi greco che si avvicinano a quello teorico:

Ora voglio modificare il programma perché vorrei impostare liberamente il numero di prove. Vorrei provare con 10000 e forse con ancor più prove.

Invochiamo la procedura così:

Interessante, no?

13.5 La generazione del pi greco mediante il pi greco…

Che cos’è un intero casuale? Può un intero scelto casualmente tra 1 e 1000000 essere realmente rappresentativo di tutti gli interi scelti casualmente? Osserviamo che il nostro esperimento è solo una approssimazione del modello ideale. Adesso modificheremo il metodo per generare numeri casuali…. Non useremo la primitiva Casuale ma genereremo numeri casuali usando la sequenza delle cifre del pi greco.
Le cifre del pi greco hanno sempre interessato i matematici:

• Le cifre da 0 a 9, ce ne sono alcune che sono più frequenti di altre?
• C’è qualche sequenza di interi che appaiono frequentemente?

In realtà sembra che la sequenza del pi greco sia veramente casuale (ancora non dimostrato). Non è possibile prevedere la cifra successiva in base alle precedenti, non c’è periodicità.
Useremo la sequenza delle cifre del pi greco per generare interi casuali:

• Come prima cosa abbiamo bisogno delle prime cifre del pi greco (per esempio un milione)
  1. Possiamo usare qualche programma che le calcoli come PiFast in ambienti Windows e SchnellPi per Linux.
  2. Oppure possiamo scaricare questo file dal sito di XLOGO:

     http://downloads.tuxfamily.org/xlogo/common/millionpi.txt

• Per generare gli interi leggeremo la sequenza di cifre in pacchetti di 7 cifre:
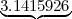  _{Primo numero 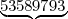Secondo numero 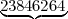Terzo numero}338327950288419716939 ecc
  
  Ho rimosso la virgola “.” in 3.14 che avrebbe causato problemi durante l’estrazione delle cifre.

Creiamo ora una nuova procedura chiamata CasualePi e modifichiamo la procedura test.

Invochiamo la procedura come al solito:

Stiamo trovato la corretta approssimazione di pi greco utilizzando le sue stesse cifre.
E’ ancora possibile migliorare il programma calcolando il tempo del calcolo. Aggiungiamo alla prima linea della procedura text:
AssegnaVar inizio SecondiDaAvvio

Quindi aggiungiamo prima di chiudere il flusso:
Stampa Frase [Tempo impiegato: ] SecondiDaAvvio - :inizio