This first example helps to understand what is a Lindenmayer system but we can’t see for now the rapport with our
turtle and LOGO..
Here it comes interesting: every word we built before has no meaning. We’re going to define for each letter of the
sequence an action to execute with the turtle, and draw with this method 2D or 3D drawing.
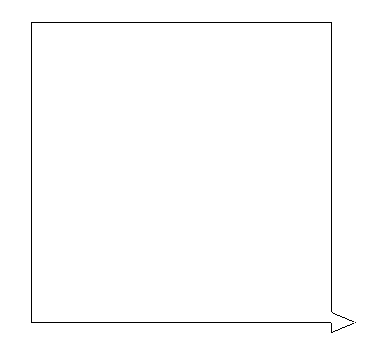
- F : Forward one unit step (
 V )
V )
- + : Turns left angle α (
 S).
S).
- - : Turns right angle α (
 S).
S).
- & : Go down angle α (
 S).
S).
- ^: Go up angle α (
 S).
S).
- \: Roll left angle α (
 S).
S).
- ∕: Roll right angle α (
 S).
S).
- |: Half-tour. In XLOGO: rt 180
For example, if α = 90 with a unit step of 10 turtle steps, we have:
|
|
|
|
|
|
|
|
|
| Symbol | F | + | - | & | ^ | \ | ∕ | | |
|
|
|
|
|
|
|
|
|
| XLOGO Command | fd 10 | lt 90 | rt 90 | down 90 | up 90 | lr 90 | rr 90 | rt 180 |
|
|
|
|
|
|
|
|
|
| |
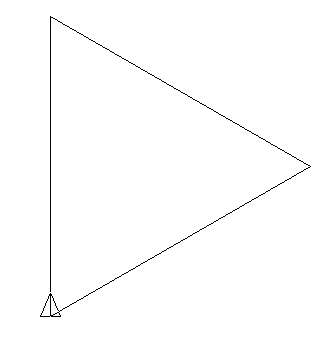
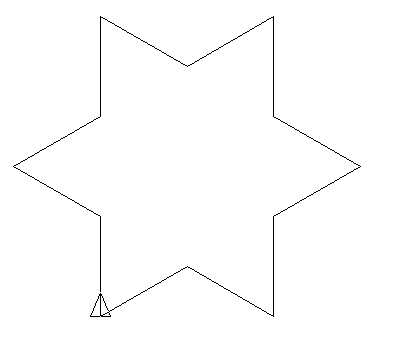
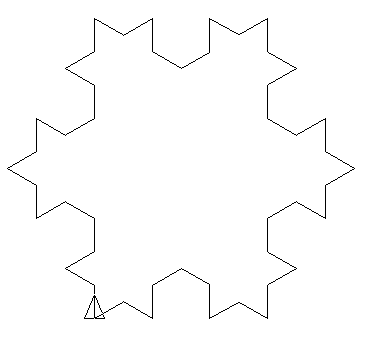
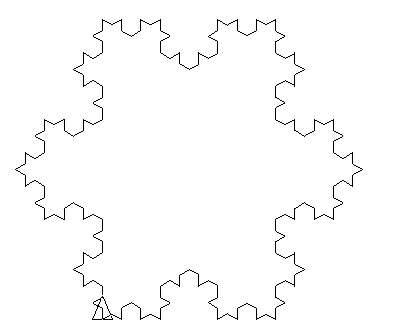
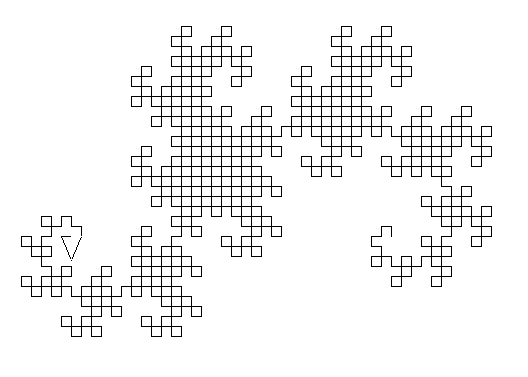
Let’s consider the L-system:
- Initial state: F --F --F --
- Production rules: F → F + F --F + F
- Angle α = 60˚, Unit step is divided by 3 between each iteration.
First iterations:
XLOGOProgram:
to snowflake :p
globalmake "unit 300/power 3 :p-1
repeat 3 [f :p-1 right 120]
end
to f :p
if :p=0 [forward :unit stop]
f :p-1 left 60 f :p-1 right 120 f :p-1 left 60
f :p-1
end
Given this new L-system:
- Initial state: F - F - F - F
- Production rules: F → F - F + F + FF - F - F + F
Here are the first representations using α = 90, we adjust the unit step for the figure has a constant size.
Then it is very easy to create a Logo program to generate these drawings:
# p represent the order
to koch :p
# Between two iteration, the unit step is divided by 4
# The final figure will have a maximal size of 600x600
globalmake "unit 300/power 4 :p-1
repeat 3 [f :p-1 left 90] f :p-1
end
# Rewriting rules
to f :p
if :p=0 [forward :unit stop]
f :p-1 left 90 f :p-1 right 90 f :p-1 right 90
f :p-1 f :p-1 left 90 f :p-1 left 90 f :p-1 right 90 f :p-1
end
- Initial state: F
- Production rules:
to a :p
if :p=0 [forward :unit stop]
a :p-1 left 90 b :p-1 left 90
end
to b :p
if :p=0 [forward :unit stop]
right 90 a :p-1 right 90 b :p-1
end
to dragon :p
globalmake "unit 300/8/ :p
a :p
end
The following example will generate a 3D Hilbert curve. This curve is singular because it fills perfectlty a cube when
we increase iterations.
Here is the L-system to consider:
- Initial state: A
- Angle α = 90˚, Unit step is divided by 2 between two iterations.
- Production rule:
|
A → B - F + CFC + F - D&F^D - F + &&CFC + F + B∕∕ |
B → A&F^CFB^F^D^^ - F - D^|F^B|FC^F^A∕∕ |
C →|D^|F^B - F + C^F^A&&FA&F^C + F + B^F^D∕∕ |
D →|CFB - F + B|FA&F^A&&FB - F + B|FC∕∕ |
|
|
to hilbert :p
clearscreen 3d
globalmake "unit 400/power 2 :p
linestart setpenwidth :unit/2
a :p
lineend
view3d
end
to a :p
if :p=0 [stop]
b :p-1 right 90 forward :unit left 90 c :p-1 forward :unit c :p-1
left 90 forward :unit right 90 d :p-1 downpitch 90 forward :unit uppitch 90 d :p-1
right 90 forward :unit left 90 downpitch 180 c :p-1 forward :unit c :p-1
left 90 forward :unit left 90 b :p-1 rightroll 180
end
to b :p
if :p=0 [stop]
a :p-1 downpitch 90 forward :unit uppitch 90 c :p-1 forward :unit b :p-1 uppitch 90
forward :unit uppitch 90 d :p-1 uppitch 180 right 90 forward :unit right 90 d :p-1
uppitch 90 right 180 forward :unit uppitch 90 b :p-1 right 180 forward :unit c :p-1
uppitch 90 forward :unit uppitch 90 a :p-1 rightroll 180
end
to c :p
if :p=0 [stop]
right 180 d :p-1 uppitch 90 right 180 forward :unit uppitch 90 b :p-1 right 90
forward :unit left 90 c :p-1 uppitch 90 forward :unit uppitch 90 a :p-1 downpitch 180
forward :unit a :p-1 downpitch 90 forward :unit uppitch 90 c :p-1 left 90 forward :unit
left 90 b :p-1 uppitch 90 forward :unit uppitch 90 d :p-1 rightroll 180
end
to d :p
if :p=0 [stop]
right 180 c :p-1 forward :unit b :p-1 right 90 forward :unit left 90 b :p-1 right 180
forward :unit a :p-1 downpitch 90 forward :unit uppitch 90 a :p-1 downpitch 180 forward :unit
b :p-1 right 90 forward :unit left 90 b :p-1 right 180 forward :unit c :p-1 rightroll 180
end
And the first iterations:
Nice, isn’t it?
 V )
V )
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).