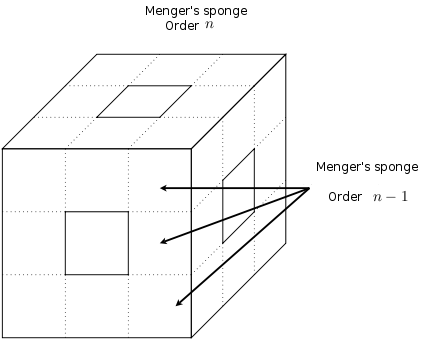
Let’s consider a Menger sponge of order n which side length is L.
On the schema, we can see that this sponge contains 20 Menger sponges of order n- 1 and with a side length 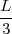 . The
recursive structure of the sponge is well shown.
. The
recursive structure of the sponge is well shown.
The program:
to cube :l
if :counter=10000 [view3d]
# faces colors
localmake "colors [yellow magenta cyan blue]
# lateral faces
repeat 4 [setpencolor run item repcount :colors square :l right 90 forward :l left 90 rightroll 90]
# bottom
setpencolor red downpitch 90 square :l uppitch 90
forward :l downpitch 90 setpencolor green square :l uppitch 90 back :l
end
to square :c
globalmake "counter :counter+1
polystart
repeat 4 [forward :c right 90]
polyend
end
# Menger’s sponge
# p: recursion order
# l: side length of the cube
to menger :l :p
if :p=0 [cube :l] [
localmake "p :p-1
localmake "l :l/3
#front face
repeat 3 [menger :l :p forward :l] back 3*:l
right 90 forward :l left 90
menger :l :p forward 2*:l menger :l :p back 2*:l
right 90 forward :l left 90
repeat 3 [menger :l :p forward :l] back 3*:l
#right face
downpitch 90 forward :l uppitch 90
menger :l :p forward 2*:l menger :l :p back 2*:l
downpitch 90 forward :l uppitch 90
repeat 3 [menger :l :p forward :l] back 3*:l
left 90 forward :l right 90
menger :l :p forward 2*:l menger :l :p back 2*:l
left 90 forward :l right 90
repeat 3 [menger :l :p forward :l] back 3*:l
downpitch 90 back :l uppitch 90
menger :l :p forward 2*:l menger :l :p back 2*:l
downpitch 90 back :l uppitch 90
]
end
to sponge :p
clearscreen hideturtle globalmake "counter 0 3d setscreencolor 0 menger 800 :p
write [nombre penpaint polygone: ] print :counter
view3d
end
This program has four procedures:
- square :c
This procedure draws a square which has side length :c. This polygon is stored in the 3D Viewer. The
variable counter counts the number of drawn polygons.
- cube :l
This procedure draws a cube which has side length :l. Of course, it uses procedure square
- menger :l :p
This is the most important procedure of the program, it draws a Menger motif of order p and with a
side length equal to l. This motif is created using recursion as we have seen before on the schema.
- sponge :p
This procedure creates a Menger sponge, order p with a side length equal to 800 and draws it in the
Viewer 3D.

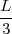 . The
recursive structure of the sponge is well shown.
. The
recursive structure of the sponge is well shown.