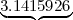 Premier nombre
Premier nombre Qu’est-ce qu’un entier aléatoire? Est-ce qu’un entier pris au hasard antre 1 et 1 000 000 est réellement représentatif d’un entier aléatoire quelconque? On s’aperçoit très vite que notre modélisation ne fait qu’approcher le modèle idéal. Bien, c’est justement sur la façon de générer le nombre aléatoire que nous allons effectuer quelques changements... Nous n’allons plus utiliser la primitive hasard mais utiliser la séquence des décimales de π. Je m’explique : les décimales de π ont toujours intrigué les mathématiciens par leur manque d’irrégularité, les chiffres de 0 à 9 semblent apparaître en quantité à peu près égales et de manière aléatoire. On ne peut prédire la prochaine décimales à l’aide des précédentes. Nous allons voir ci-après comment générer un nombre alatoire à l’aide des décimales de π. Tout d’abord, il va vous falloir récupérer les premières décimales de pi (par exemple un million).
http ://downloads.tuxfamily.org/xlogo/common/millionpi.txt |
Pour créer nos nombres aléatoires, bous prendrons des paquets de 8 chiffres dans la suite des décimales de π.
Explication, le fichier commence ainsi :
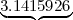 Premier nombre
Premier nombre
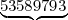 Deuxième nombre
Deuxième nombre
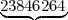 Troisième nombre338327950288419716939
etc
Troisième nombre338327950288419716939
etc
J’enlève le « . »du 3.14 .... qui risque de nous ennuyer quand on extraiera les décimales. Bien, tout est en place, nous créons une nouvelle procédure appelée hasardpi et modifions légèrement la procédure test
pour pgcd :a :b
si (reste :a :b)=0 [retourne :b][retourne pgcd :b reste :a :b]
fin
pour test :essais
# On ouvre un flux repéré par le chiffre 1 vers le fichier millionpi.txt
# (ici, supposé être dand le répertoire courant
# sinon utiliser fixerepertoire et un chemin absolu)
ouvreflux 1 "millionpi.txt
# Affecte à la variable ligne la première ligne du fichier millionpi.txt
donne "ligne premier lisligneflux 1
# On initialise la variable compteur à 0
donne "compteur 0
repete :essais [
si 1=pgcd hasardpi 7 hasardpi 7 [donne "compteur :compteur+1]
]
# On calcule la frequence
donne "f :compteur/:essais
# On affiche la valeur approchée de pi
ecris phrase [approximation de pi:] racine (6/:f)
fermeflux 1
fin
pour hasardpi :n
soit "nombre "
repete :n [
# S’il n’y plus de caractere sur la ligne
si 0=compte :ligne [donne "ligne premier lisligneflux 1]
# On donne à la variable caractere la valeur du premier caractere de la ligne
donne "caractere premier :ligne
# puis on enleve ce premier caractere de la ligne.
donne "ligne saufpremier :ligne
donne "nombre mot :nombre :caractere
]
retourne :nombre
fin
test 10
approximation de pi: 3.4641016151377544
test 100
approximation de pi: 3.1108550841912757
test 1000
approximation de pi: 3.081180112566604
test 10000
approximation de pi: 3.1403714651066386
test 70000
approximation de pi: 3.1361767950325627
|
On retrouve donc une approximation du nombre π à l’aide de ses propres décimales!
Il est encore possible d’améliorer ce programme en indiquant par exemple le temps mis pour le calcul. On rajoute
alors en première ligne de la procedure test :
donne "debut temps
On rajoute juste avant fermeflux 1 :
ecris phrase [Temps mis : ] temps - :debut