 ≈ 0,6079. To exhibit this result, we’re going to:
≈ 0,6079. To exhibit this result, we’re going to: In fact, a famous result in numbers theory says that the probability for two randomly chosen integers to be coprime
is  ≈ 0,6079. To exhibit this result, we’re going to:
≈ 0,6079. To exhibit this result, we’re going to:
to test # We set the variable counter to 0 globalmake "counter 0 repeat 1000 [ if (gcd random 1000000 random 1000000)=1 [globalmake "counter :counter+1] ] print [frequence:] print :counter/1000 end |
In a similar way as the precevious note, notice the parenthesis around gcd random 1000000 random 1000000.
Otherwise, the interpreter will try to evaluate 1 000 000 = 1. You can write in other way: if 1=gcd random
1000000 random 1000000
We execute the program test.
test
0.609
test
0.626
test
0.597
|
We obtain some values close to the theorical probability: 0,6097. This frequency is an approximation of
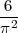 .
.
Thus, if I note f the frequency, we have: f ≈
Hence, π2 ≈ and π ≈
and π ≈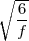 .
.
I append to my program a line that gives this π approximation in procedure test:
to test # We set the variable counter to 0 globalmake "counter 0 repeat 1000 [ if (gcd random 1000000 random 1000000)=1 [globalmake "counter :counter+1] ] # We calculate te frequency make "f :counter/1000 # we dispaly the pi approximation print sentence [ pi approximation:] sqrt (6/:f) end test pi approximation: 3.1033560252704917 test pi approximation: 3.1835726998350666 test pi approximation: 3.146583877637763 |
Now, we modify the program because I want to set the number of tries. I want to try with 10 000 and perhaps more tries.
to test :tries
# We set the variable counter to 0
globalmake "counter 0
repeat :tries [
if (gcd random 1000000 random 1000000)=1 [globalmake "counter :counter+1]
]
# We calculate te frequency
make "f :counter/:tries
# we dispaly the pi approximation
print sentence [ pi approximation:] sqrt (6/:f)
end
test 10000
pi approximation: 3.1426968052735447
test 10000
pi approximation: 3.1478827771265787
test 10000
pi approximation: 3.146583877637763
test 10000
|
Quite interesting, isn’t it?