9.6 π Approximation

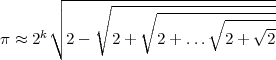
approximation We can approximate the number π using the formula:

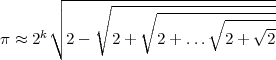
┌│ ---∘-----∘----------------- │∘ ∘ ----√--- π ≈ 2k 2− 2 + 2 + ... 2 + 2
with k the number of squareroots. The greater is k, the better is the π .



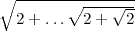The formula contains the recursive expression 2 + ∘ --------------- ∘ ---√--- 2 + ... 2+ 2, so let’s code: 
 # k is the number of squareroots
 to approxpi :k
 write "approximation:\  print (power 2 :k) * squareroot (2- squareroot (calc :k-2))
 print "-------------------------
 write "pi:\  print pi
 end
 
 to calc :p
 if :p=0 [output 2][output 2+squareroot calc :p-1]
 end
 
 approxpi 10
 Approximation: 3.141591421568446
 -------------------------
 Pi: 3.141592653589793

We found the first 5 digits! If we’re looking for more π digits, we have to allow a better precision with a higher number of digits while computing. Thus, we’re going to use the primitive setdigits. 

 setdigits 100
 approxpi 100
 Approximation: 3.1415926535897932384626433832795028841973393069670160975807684313880468...
 -------------------------
 Pi: 3.141592653589793238462643383279502884197169399375105820974944592307816406....

And now, we have 39 digits...